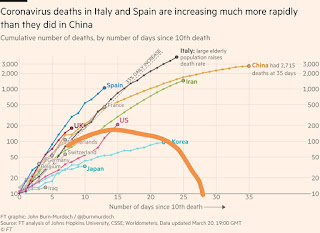
In deze post probeer ik op basis van beschikbare data een toekomst beeld te schetsen van hoe deze pandemie zich gaat ontwikkelen.
Disclaimers
Ik ben geen expert.
Niemand kan de toekomst voorspellen.
Ik hoop dat niemand aan het Coronavirus dood gaat.
Er zijn miljoenen parameters waar je rekening mee moet houden om iets te kunnen voorspellen. Helaas ken ik deze miljoenen parameters niet en daarom kan ik ze dus ook niet in mijn berekeningen meenemen. Ik weet echter wel wat de belangrijkste parameters zijn en ik probeer me op die parameters te focussen om een goede schatting te maken.
De belangrijkste parameters.
Zoals hierboven al staat omschreven focus ik alleen op de belangrijkste knoppen waar je aan kan draaien om het uiteindelijke getal significant te beinvloeden. Ieder land heeft zijn eigen lijn, maar er is altijd een duidelijke mediaan te zien, en van die mediaan wordt slechts een klein beetje afgeweken. Enkele tientallen doden meer of minder gaat het (helaas) niet om, het gaat om the bigger picture. De belangrijkste parameters die ik in mijn berekeningen meeneem, en waarvan ik dus zeg dat je hiermee het uiteindelijke dodental significant kan beinvloeden zijn de volgende:
- Aantal beschikbare IC bedden
- Datum van lockdown
- Naleving van lockdown
De lijn die ik trek is enkel gebaseerd op het dodental dat per land gepubliceert wordt. Deze waarde blijkt namelijk de meest betrouwbare waarde op dit moment. Bij iemand die overlijdt moet namelijk altijd de doodsoorzaak worden vastgestelt, dit verschilt iets per land, maar niet heel veel. Alleen bij Duitsland lijkt het dodental niet te kloppen.
Wishful thinking
Wat ik veel zie op dit moment is wishful thinking. Een eigenschap van de mens om overal het positieve te zien. Als we een chimpansee een hand zien uitsteken naar een man die in het water ligt denken wij te zien: "Een dier dat een mensenleven redt". En niet een dier dat gewendt is een banaan van een mens te krijgen om op te eten. Ik doe niet aan wensdenken en ik focus alleen maar op data. Als ik aan wensdenken zou doen is dit de grafiek die ik zou tekenen, en gelukkig begrijpen de meeste mensen dat deze grafiek nergens op slaat.
Kenmerken van dit virus
Een virus maakt geen onderscheidt tussen ras, leeftijd, geslacht en salaris. Iedereen kan het virus krijgen.
Onderaan deze blog vertel ik waarom ik sommige kenmerken van de virus oversla.
De data
De data die ik gebruik zijn het aantal doden per land. Deze waarden blijken namelijk bijzonder goed gelijk te lopen. Als nul punt gebruik ik het moment dat een land 50 doden heeft. Het eerste slachtoffer kan namelijk heel willekeurig zijn, maar 50 sterfgevallen zorgt al meer voor een gemiddelde afspiegeling van de infectiegraad van de bevolking.
Onderaan deze blog vertel ik waarom ik sommige data niet meeneem.
Voorspellingen
Als we deze statistieken invoeren is Italie koploper. Italie zal bepalen wanneer de lockdown maatregelen zichtbaar gaan worden in het dodental per dag. Wanneer we de relevante data in een tabel zetten krijgen we de volgende:
Disclaimers
Ik ben geen expert.
Niemand kan de toekomst voorspellen.
Ik hoop dat niemand aan het Coronavirus dood gaat.
Er zijn miljoenen parameters waar je rekening mee moet houden om iets te kunnen voorspellen. Helaas ken ik deze miljoenen parameters niet en daarom kan ik ze dus ook niet in mijn berekeningen meenemen. Ik weet echter wel wat de belangrijkste parameters zijn en ik probeer me op die parameters te focussen om een goede schatting te maken.
De belangrijkste parameters.
Zoals hierboven al staat omschreven focus ik alleen op de belangrijkste knoppen waar je aan kan draaien om het uiteindelijke getal significant te beinvloeden. Ieder land heeft zijn eigen lijn, maar er is altijd een duidelijke mediaan te zien, en van die mediaan wordt slechts een klein beetje afgeweken. Enkele tientallen doden meer of minder gaat het (helaas) niet om, het gaat om the bigger picture. De belangrijkste parameters die ik in mijn berekeningen meeneem, en waarvan ik dus zeg dat je hiermee het uiteindelijke dodental significant kan beinvloeden zijn de volgende:
- Aantal beschikbare IC bedden
- Datum van lockdown
- Naleving van lockdown
De lijn die ik trek is enkel gebaseerd op het dodental dat per land gepubliceert wordt. Deze waarde blijkt namelijk de meest betrouwbare waarde op dit moment. Bij iemand die overlijdt moet namelijk altijd de doodsoorzaak worden vastgestelt, dit verschilt iets per land, maar niet heel veel. Alleen bij Duitsland lijkt het dodental niet te kloppen.
Wishful thinking
Wat ik veel zie op dit moment is wishful thinking. Een eigenschap van de mens om overal het positieve te zien. Als we een chimpansee een hand zien uitsteken naar een man die in het water ligt denken wij te zien: "Een dier dat een mensenleven redt". En niet een dier dat gewendt is een banaan van een mens te krijgen om op te eten. Ik doe niet aan wensdenken en ik focus alleen maar op data. Als ik aan wensdenken zou doen is dit de grafiek die ik zou tekenen, en gelukkig begrijpen de meeste mensen dat deze grafiek nergens op slaat.
Kenmerken van dit virus
Een virus maakt geen onderscheidt tussen ras, leeftijd, geslacht en salaris. Iedereen kan het virus krijgen.
Onderaan deze blog vertel ik waarom ik sommige kenmerken van de virus oversla.
De data
De data die ik gebruik zijn het aantal doden per land. Deze waarden blijken namelijk bijzonder goed gelijk te lopen. Als nul punt gebruik ik het moment dat een land 50 doden heeft. Het eerste slachtoffer kan namelijk heel willekeurig zijn, maar 50 sterfgevallen zorgt al meer voor een gemiddelde afspiegeling van de infectiegraad van de bevolking.
Onderaan deze blog vertel ik waarom ik sommige data niet meeneem.
Voorspellingen
Als we deze statistieken invoeren is Italie koploper. Italie zal bepalen wanneer de lockdown maatregelen zichtbaar gaan worden in het dodental per dag. Wanneer we de relevante data in een tabel zetten krijgen we de volgende:
| Land | Lockdown | IC bedden per 100k | Total IC bedden | bron |
| IT | 09-03-2020 | 12.5 | 7500 | [bron] |
| ES | 15-03-2020 | 9.7 | 4500 | [bron] |
| FR | 16-03-2020 | 11.6 | 8000 | [bron] |
| US | - | 34.7 | 120000 | [bron] |
| UK | - | 6.6 | 4500 | [bron] |
| NL | 15-03-2020 | 6.4 | 1250 | [bron] |
Nu kunnen we 2 tabellen maken, een met aantal doden per 100.000 inwoners en een met doden totaal. Op dit moment is doden per 100.000 nog niet interessant omdat we nu nog puur in de groei fase van het virus zitten. In geen enkele tabel is de maatregelen van de lockdown meetbaar, dus die grafiek sla ik voor nu even over en ik focus me enkel en alleen op de groei van het aantal doden per land. Die groei wordt namelijk puur en -alleen- bepaald door het virus. Het virus is in ieder land exact hetzelfde. Dit zou dus ook zichtbaar moeten zijn in de getallen. Ik probeer de getallen gelijk te laten lopen en begin ongeveer bij 50 doden. Je ziet dat alle tabellen dan verassend gelijke aantallen hebben.
| Dagen | Nederland | Italy | France | Spain | US | UK |
| 1 | 59 | 52 | 75 | 36 | 56 | 55 |
| 2 | 77 | 79 | 91 | 55 | 62 | 71 |
| 3 | 107 | 107 | 127 | 86 | 75 | 103 |
| 4 | 137 | 148 | 148 | 133 | 96 | 144 |
| 5 | 197 | 175 | 196 | 122 | 191 | |
| 6 | 233 | 244 | 294 | 172 | ||
| 7 | 366 | 372 | 342 | 221 | ||
| 8 | 463 | 450 | 533 | 280 | ||
| 9 | 631 | 638 | ||||
| 10 | 827 | 833 | ||||
| 11 | 1016 | 1093 | ||||
| 12 | 1266 | 1378 | ||||
| 13 | 1441 | |||||
| 14 | 1809 | |||||
| 15 | 2158 | |||||
| 16 | 2503 | |||||
| 17 | 2978 | |||||
| 18 | 3405 | |||||
| 19 | 4032 | |||||
| 20 | 4825 |
Om een voorspelling te doen kunnen we een gemiddelde nemen van de andere landen die op dezelfde positie in de tabel zitten. Als we data extrapoleren vanuit de andere tabellen en zo berekenen welke getallen Nederland vandaag gaat krijgen komen we uit op: minimaal 122 en maximaal 197 of een gemiddelde van 176.
Dit werkt echter niet bij Italie omdat dat de koploper is. Als we de nieuwe data voor Italie willen bereken kunnen we kijken naar het gemiddelde stijgings percentage, hieronder weergeven.
Dat is 29%. Om een trend breuk te veroorzaken moet de stijging onder de 14% komen of boven de 57%. Nemen we die 2 waarden om een volgend punt te bepalen komen we op de volgende twee getallen: 675 en 2750. Het ligt dus in de lijn der verwachting dat het nieuwe dodental in Italie morgen tussen de 675 en 2750 ligt, door de exponentiele groei enorm ruime getallen. Het gemiddelde getal, 29% stijging is 1400. Maar zoals duidelijk in de grafiek te zien is vlakt dat percentage lichtelijk af. Pakken we de laatste 10 data punten dan zitten we op een gemiddelde van 20% en dat zou 965 nieuwe doden betekenen.
Op deze manier kunnen we voor alle landen bepalen wat het nieuwe getal ongeveer worden.
Voor nu ga ik deze 2 methoden (wanneer mogelijk) toepassen op Italie, Spanje, Frankrijk, Nederland, Amerika en het VK om het aantal doden te voorspellen van morgen.
Methode 1 is op basis van data van andere landen, methode 2 is minimum stijging percentage, maximum stijging en de mediaan.
De volgende getallen komen daaruit:
Methode 1 (Totaal aantal doden)
Methode 2 (Aantal nieuwe doden)
Italie:
Spanje:
Frankrijk
Nederland
US
UK
Kenmerken van dit virus
Een virus maakt geen onderscheidt tussen ras, leeftijd, geslacht en salaris. Iedereen kan het virus krijgen. De een reageert er lichamelijk alleen anders op dan de ander. En deze reactie heeft weer invloed op de besmettelijkheid. Iemand met veel virusdeeltjes in zijn lichaam verspreid meer deeltjes wanneer hij niest dan iemand met weinig deeltjes in zijn lichaam. Iemand met weinig deeltjes in zijn lichaam die veel mensen ontmoet heeft nog steeds een hoge kans op verspreiding. En iemand met heel weinig deeltjes in zijn lichaam die aan alles en iedereen likt heeft al helemaal een hoge kans op verspreiding. De formule voor verspreiding is dus:
a = aantal aanwezige deeltjes, b = contact punten, c = hygiene.
Kinderen & Studenten hebben slechte hygiene, veel contact punten en weinig deeltjes.
Jong/Volwassenen hebben goede hygiene, veel contact punten en weinig deeltjes.
Ouderen hebben goede hygiene, weinig contact punten en veel deeltjes.
Iedere groep lijkt iets te hebben, en daarom neem ik leeftijd in deze berekeningen -niet- mee.
De data
Er is bijzonder veel data beschikbaar op dit moment. Er worden overal test resultaten gepubliceerd van geinfecteerde personen, herstelde personen en dodentallen. Elk land heeft een eigen manier van meten en testen dus we moeten proberen hier een vast patroon in te herkennen.
Idealiter hebben we een meting van -alle- personen in een land, en dat -iedere- dag. Die data is er helaas niet, dus moeten we de meest betrouwbare data pakken. Voor de hand ligt het om te kiezen voor het aantal infecties per dag. Maar die data is duidelijk geen weerspiegeling van de bevolking, kijken we bijvoorbeeld naar Nederland dan is volgens de data van het RIVM 25% een zorgmedewerker. We weten allemaal dat dat niet zo is, en dat zorgmedewerkers vaker in de testen van het RIVM voorkomen omdat zorgmedewerkers vaker getest worden. Een ander voorbeeld van een duidelijk verschil in testen: In Nederland is 42% van de geteste mensen 60+, in Duitsland is dat 16% [bron]. Omdat die waarden overal compleet anders gemeten worden en de waarden dermate veel van elkaar afwijken beschouw ik deze als -niet- betrouwbaar en negeer ik ze compleet.
De data die ik gebruik zijn het aantal doden per land. Deze waarden blijken namelijk bijzonder goed gelijk te lopen. Als nul punt gebruik ik het moment dat een land 50 doden heeft. Het eerste slachtoffer kan namelijk heel willekeurig zijn, maar 50 sterfgevallen zorgt al meer voor een gemiddelde afspiegeling van de infectiegraad van de bevolking.
Voor nu ga ik deze 2 methoden (wanneer mogelijk) toepassen op Italie, Spanje, Frankrijk, Nederland, Amerika en het VK om het aantal doden te voorspellen van morgen.
Methode 1 is op basis van data van andere landen, methode 2 is minimum stijging percentage, maximum stijging en de mediaan.
De volgende getallen komen daaruit:
Methode 1 (Totaal aantal doden)
| Country | min | max | avg |
| NL | 122 | 197 | 176.2 |
| UK | 172 | 294 | 235.75 |
| FR | 631 | 638 | 634.5 |
| US | 631 | 638 | 634.5 |
Methode 2 (Aantal nieuwe doden)
Italie:
| min | 14% | 675.5 |
| max | 57% | 2750.25 |
| avg l 10 | 20% | 965 |
| avg | 29% | 1399.25 |
Spanje:
| min | 16% | 220.48 |
| max | 55% | 757.9 |
| avg | 38% | 523.64 |
| avg 10 | 34% | 468.52 |
Frankrijk
| min | 17% | 76.5 |
| max | 54% | 243 |
| avg | 30% | 135 |
Nederland
| min | 28% | 38.08 |
| max | 39% | 53.04 |
| avg | 33% | 44.88 |
US
| min | 14% | 39.2 |
| max | 41% | 114.8 |
| avg | 24% | 67.2 |
UK
| min | 23% | 56.12 |
| max | 45% | 109.8 |
| avg | 35% | 85.4 |
Kenmerken van dit virus
Een virus maakt geen onderscheidt tussen ras, leeftijd, geslacht en salaris. Iedereen kan het virus krijgen. De een reageert er lichamelijk alleen anders op dan de ander. En deze reactie heeft weer invloed op de besmettelijkheid. Iemand met veel virusdeeltjes in zijn lichaam verspreid meer deeltjes wanneer hij niest dan iemand met weinig deeltjes in zijn lichaam. Iemand met weinig deeltjes in zijn lichaam die veel mensen ontmoet heeft nog steeds een hoge kans op verspreiding. En iemand met heel weinig deeltjes in zijn lichaam die aan alles en iedereen likt heeft al helemaal een hoge kans op verspreiding. De formule voor verspreiding is dus:
a = aantal aanwezige deeltjes, b = contact punten, c = hygiene.
Kinderen & Studenten hebben slechte hygiene, veel contact punten en weinig deeltjes.
Jong/Volwassenen hebben goede hygiene, veel contact punten en weinig deeltjes.
Ouderen hebben goede hygiene, weinig contact punten en veel deeltjes.
Iedere groep lijkt iets te hebben, en daarom neem ik leeftijd in deze berekeningen -niet- mee.
De data
Er is bijzonder veel data beschikbaar op dit moment. Er worden overal test resultaten gepubliceerd van geinfecteerde personen, herstelde personen en dodentallen. Elk land heeft een eigen manier van meten en testen dus we moeten proberen hier een vast patroon in te herkennen.
Idealiter hebben we een meting van -alle- personen in een land, en dat -iedere- dag. Die data is er helaas niet, dus moeten we de meest betrouwbare data pakken. Voor de hand ligt het om te kiezen voor het aantal infecties per dag. Maar die data is duidelijk geen weerspiegeling van de bevolking, kijken we bijvoorbeeld naar Nederland dan is volgens de data van het RIVM 25% een zorgmedewerker. We weten allemaal dat dat niet zo is, en dat zorgmedewerkers vaker in de testen van het RIVM voorkomen omdat zorgmedewerkers vaker getest worden. Een ander voorbeeld van een duidelijk verschil in testen: In Nederland is 42% van de geteste mensen 60+, in Duitsland is dat 16% [bron]. Omdat die waarden overal compleet anders gemeten worden en de waarden dermate veel van elkaar afwijken beschouw ik deze als -niet- betrouwbaar en negeer ik ze compleet.
De data die ik gebruik zijn het aantal doden per land. Deze waarden blijken namelijk bijzonder goed gelijk te lopen. Als nul punt gebruik ik het moment dat een land 50 doden heeft. Het eerste slachtoffer kan namelijk heel willekeurig zijn, maar 50 sterfgevallen zorgt al meer voor een gemiddelde afspiegeling van de infectiegraad van de bevolking.
Kantel punten qua IC bedden en doden.